Finite Intelligence Will Strive Towards Divergence
Finite Intelligence Will Strive Towards Divergence
Finite Intelligence Will Strive Towards Divergence
Written by
Written by
Written by
Walter De Brouwer
Walter De Brouwer
Posted on
Posted on
Posted on
Jun 20, 2025
Jun 20, 2025
Jun 20, 2025
Read
Read on Substack
Read on Substack
Intelligence will continuously expand into uncharted territories
— akin to a mathematical divergent series whose sum never conventionally converges.
Unlike a neatly convergent series (example of a geometric series ½ + ¼ + ⅛…), intelligence behaves more like a divergent harmonic series
(1 + ½ + ⅓ + ¼ + …), seemingly infinite and boundless. Even though the terms being added are getting smaller and smaller, the sum itself continues to grow without bound.
It grows very slowly, but it does indeed go to infinity.
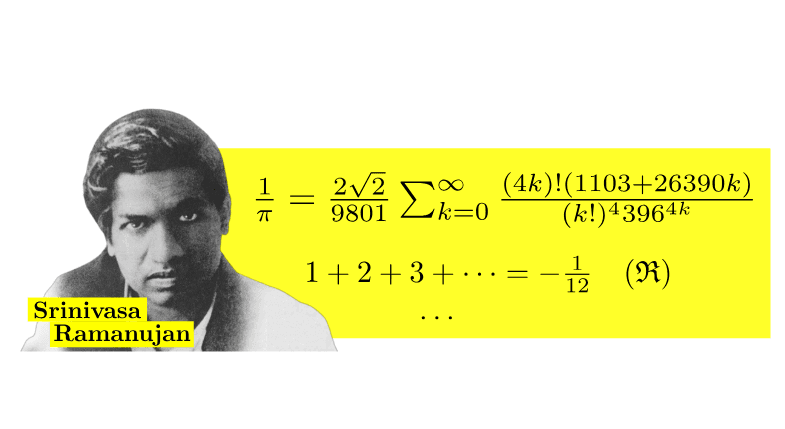
Yet, just as Ramanujan summation surprisingly assigns finite, meaningful values to divergent series — famously demonstrating, for example, that 1 + 2 + 3 + 4 + ... equals -1/12 — so too might intelligence and understanding converge unexpectedly into a coherent, profound form we now imagine to be Artificial General Intelligence (AGI).
Thus, the seemingly limitless complexity of neural networks could
ultimately yield AGI through an analogous form of convergence, challenging our traditional views of intellectual and computational boundaries.
Therefore however, we would need to arrive at some steps in the evolution
of models which are now only theoretical.
For instance, predicting phase-transition points in scaling laws (e.g. sudden jumps in capability) would help or Designing architectures that explicitly exploit complex or continuous hyperparameter trajectories. But we lack closed-form “generating functions” for network behavior in width/depth/data, so constructing true analytic extensions is highly speculative. Even if mathematically defined, realizing these continuations in practice
(training algorithms, numerical stability) remains an open engineering challenge.
Tentative next steps would be:
Find an analytic surrogate
for training dynamics—e.g. a function H(n,d,t)H(n,d,t)H(n,d,t) for width nnn, depth ddd, and training time ttt.Prove or empirically validate that HHH admits an analytic continuation beyond its “natural” domain.
Experiment with complex-valued nets or continuous-depth flows to see if new capabilities emerge off the beaten path.
An “analytic-continuation operator” for neural nets would amount to recasting network architectures, hyperparameters,
or training processes as genuinely analytic functions of some continuous
(or complex) variables— and then exploring those extended domains for emergent structure.
While the math isn’t there yet, pushing in these directions could uncover the very principle that lets AGI “sum up” from today’s divergent, overparameterized models.
Intelligence will continuously expand into uncharted territories
— akin to a mathematical divergent series whose sum never conventionally converges.
Unlike a neatly convergent series (example of a geometric series ½ + ¼ + ⅛…), intelligence behaves more like a divergent harmonic series
(1 + ½ + ⅓ + ¼ + …), seemingly infinite and boundless. Even though the terms being added are getting smaller and smaller, the sum itself continues to grow without bound.
It grows very slowly, but it does indeed go to infinity.
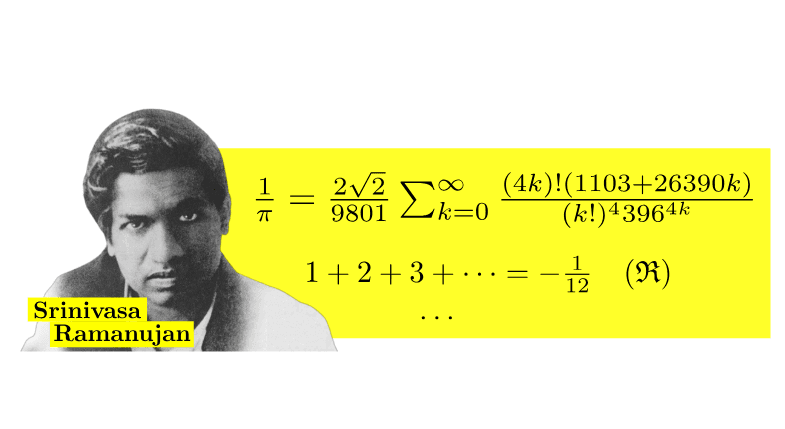
Yet, just as Ramanujan summation surprisingly assigns finite, meaningful values to divergent series — famously demonstrating, for example, that 1 + 2 + 3 + 4 + ... equals -1/12 — so too might intelligence and understanding converge unexpectedly into a coherent, profound form we now imagine to be Artificial General Intelligence (AGI).
Thus, the seemingly limitless complexity of neural networks could
ultimately yield AGI through an analogous form of convergence, challenging our traditional views of intellectual and computational boundaries.
Therefore however, we would need to arrive at some steps in the evolution
of models which are now only theoretical.
For instance, predicting phase-transition points in scaling laws (e.g. sudden jumps in capability) would help or Designing architectures that explicitly exploit complex or continuous hyperparameter trajectories. But we lack closed-form “generating functions” for network behavior in width/depth/data, so constructing true analytic extensions is highly speculative. Even if mathematically defined, realizing these continuations in practice
(training algorithms, numerical stability) remains an open engineering challenge.
Tentative next steps would be:
Find an analytic surrogate
for training dynamics—e.g. a function H(n,d,t)H(n,d,t)H(n,d,t) for width nnn, depth ddd, and training time ttt.Prove or empirically validate that HHH admits an analytic continuation beyond its “natural” domain.
Experiment with complex-valued nets or continuous-depth flows to see if new capabilities emerge off the beaten path.
An “analytic-continuation operator” for neural nets would amount to recasting network architectures, hyperparameters,
or training processes as genuinely analytic functions of some continuous
(or complex) variables— and then exploring those extended domains for emergent structure.
While the math isn’t there yet, pushing in these directions could uncover the very principle that lets AGI “sum up” from today’s divergent, overparameterized models.
Intelligence will continuously expand into uncharted territories
— akin to a mathematical divergent series whose sum never conventionally converges.
Unlike a neatly convergent series (example of a geometric series ½ + ¼ + ⅛…), intelligence behaves more like a divergent harmonic series
(1 + ½ + ⅓ + ¼ + …), seemingly infinite and boundless. Even though the terms being added are getting smaller and smaller, the sum itself continues to grow without bound.
It grows very slowly, but it does indeed go to infinity.
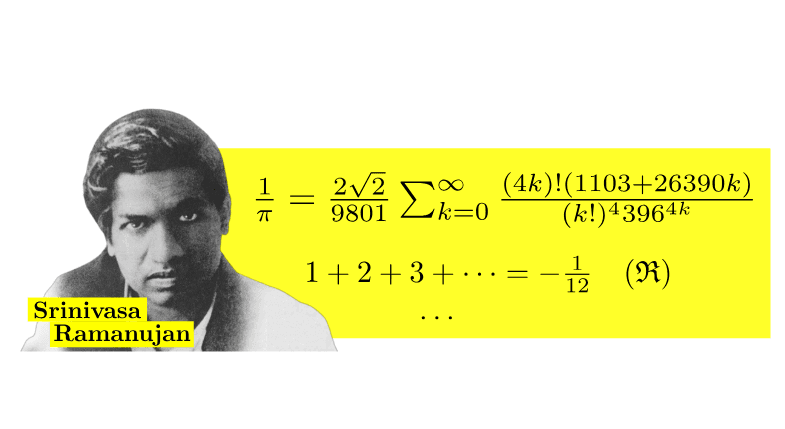
Yet, just as Ramanujan summation surprisingly assigns finite, meaningful values to divergent series — famously demonstrating, for example, that 1 + 2 + 3 + 4 + ... equals -1/12 — so too might intelligence and understanding converge unexpectedly into a coherent, profound form we now imagine to be Artificial General Intelligence (AGI).
Thus, the seemingly limitless complexity of neural networks could
ultimately yield AGI through an analogous form of convergence, challenging our traditional views of intellectual and computational boundaries.
Therefore however, we would need to arrive at some steps in the evolution
of models which are now only theoretical.
For instance, predicting phase-transition points in scaling laws (e.g. sudden jumps in capability) would help or Designing architectures that explicitly exploit complex or continuous hyperparameter trajectories. But we lack closed-form “generating functions” for network behavior in width/depth/data, so constructing true analytic extensions is highly speculative. Even if mathematically defined, realizing these continuations in practice
(training algorithms, numerical stability) remains an open engineering challenge.
Tentative next steps would be:
Find an analytic surrogate
for training dynamics—e.g. a function H(n,d,t)H(n,d,t)H(n,d,t) for width nnn, depth ddd, and training time ttt.Prove or empirically validate that HHH admits an analytic continuation beyond its “natural” domain.
Experiment with complex-valued nets or continuous-depth flows to see if new capabilities emerge off the beaten path.
An “analytic-continuation operator” for neural nets would amount to recasting network architectures, hyperparameters,
or training processes as genuinely analytic functions of some continuous
(or complex) variables— and then exploring those extended domains for emergent structure.
While the math isn’t there yet, pushing in these directions could uncover the very principle that lets AGI “sum up” from today’s divergent, overparameterized models.
All blogs

